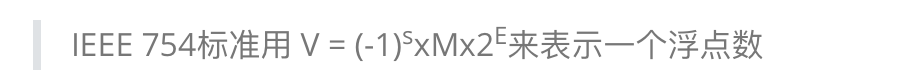浮点型简单讲就是实数的意思。浮点数在计算机中用以近似表示任意某个实数。具体的说,这个实数由一个整数或定点数(即尾数)乘以某个基数(计算机中通常是 2)的整数次幂得到,这种表示方法类似于基数为 10 的科学记数法。
目前计算机在表示浮点数是采用IEEE 754标准,该标准的诞生为科学应用程序在不同机器上的可移植性奠定了基础
IEEE 754标准
- 符号位s,决定这是一个正数还是一个负数。当s=0时为正数,s=1时为负数
- M位,即有效数字位,该值是一个二进制小数,它的范围是大于1小于2
- E指数位,又称阶码位,作用是对浮点数进行加权
IEEEE 754规定,数字系统中的浮点数是对数学中小数的近似,同时规定表达浮点数的0,1序列被分为三部分
规则示例(3.14的表示)
- 首先将十进制小数转成二进制小数11.0010001111010111
- 将二进制小数转为IEEE浮点数标准格式,即1.10010001111010111x21
- 对照上图,sign符号位为0,表示正数,exponent表示科学计数法的指数部分(这里的指数并不是计算出来的指数,而是计算出来的指数加上偏移量,对于32位单精度浮点数来说,偏移值为127,所以component的值为127+1=128),二进制表示为10000000。
- fraction表示有效数字位,又叫尾数。即10010001111010111。再补齐只23位,即10010001111010111000000
- 因此32位单精度浮点数3.14在计算机中被表示为:0 10000000 10010001111010111000000
对于64位双精度浮点数来说,exponent段为11位,偏移值为1023,fraction长度为52位
浮点运算就是实数运算,主要运用在科学和多媒体中,可以理解为小数点可移动的运算方式。
单精度浮点数也就是float,用4个字节来存储的,单精度小数点后面共能精确到7位小数。单精度浮点运算应用在图形应用程序graphics application,图像处理image processing,机器学习。大部分人工智能训练任务以单精度浮点数或半精度浮点数为主,推理以Int8为主。
双精度double是用8个字节来存储的,双精度可精确到15位小数。双精度浮点运算主要用于超算领域。
实际应用中,单精度和双精度浮点运算是综合使用的,超算会根据需要分配单双精度,模拟(化学、物理、金融),数值分析等科学计算。
本站部分文章来源或改编自互联网及其他公众平台,主要目的在于分享信息,版权归原作者所有,内容仅供读者参考。本站仅提供信息存储空间服务,如有侵权请联系我们删除。如若转载,请注明出处:https://sndnote.com/tougao/38736.html